El problema de Monty Hall

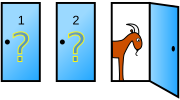
Imagina que estás en un concurso donde se te ofrece escoger entre tres puertas: detrás de una de ellas hay un Lamborghini Mutciélago y detrás de las otras hay cabras. Escoges una puerta, digamos la nº1, y el presentador, que sabe lo que hay detrás de cada puerta abre otra, digamos la nº3, que contiene una cabra. Entonces el presentador te pregunta: "¿No prefieres cambiar tu respuesta y escoger la nº2?".

¿Dónde es más probable que se encuentre el automóvil?

SOLUCION

La probabilidad de que el concursante escoja en su primera oportunidad la puerta que oculta el coche es de 1/3, por lo que la probabilidad de que el coche se encuentre en una de las puertas que no ha escogido es de 2/3. ¿Qué cambia cuando el presentador muestra una cabra tras una de las otras dos puertas?

Una suposición errónea es que, una vez sólo queden dos puertas, ambas tienen la misma probabilidad (un 50%) de contener el coche. Es errónea ya que el presentador abre la puerta después de la elección de jugador. Esto es, la elección del jugador afecta a la puerta que abre el presentador. No es un suceso aleatorio ni inconexo.

Si el jugador escoge en su primera opción la puerta que contiene el coche (con una probabilidad de 1/3), entonces el presentador puede abrir cualquiera de las dos puertas. Además, el jugador pierde el coche si cambia cuando se le ofrece la oportunidad.

Pero, si el jugador escoge una cabra en su primera opción (con una probabilidad de 2/3), el presentador sólo tiene la opción de abrir una puerta, y esta es la única puerta restante que contiene una cabra. En ese caso, la puerta restante tiene que contener el coche, por lo que cambiando lo gana.

En resumen, si mantiene su elección original gana si escogió originalmente el coche (con probabilidad de 1/3), mientras que si cambia, gana si escogió originalmente una de las dos cabras (con probabilidad de 2/3). Por lo tanto, el concursante debe cambiar su elección si quiere maximizar la probabilidad de ganar el coche.

Para matemáticos: Sea X:(Omega, P) → {1,2,3} la puerta aleatoria detrás de la cual se encuentra el coche. Sea Y:(Omega, P) → {1,2,3} la puerta que escoge aleatoriamente el candidato. Las variables aleatorias X e Y son estocásticamente independientes. Sea M: (Omega, P) → {cabra, coche} lo que se encuentra detrás de la puerta que el moderador, de manera aleatoria, escoge (entre las que aún no se han abierto). Se cumple entonces [M=cabra] con probabilidad 1 (o siempre). La probabilidad que el candidato se lleve el coche bajo el supuesto que él no cambia de puerta es entonces P[X=Y|M=cabra]=P[X=Y]=1/3. La probabilidad que el candidato se lleve el coche bajo el supuesto que él cambia de puerta es entonces P[X≠Y|M=cabra]=1-P[X=Y]=2/3. (Esta es la solución correcta.)

Una solución incorrecta se obtiene de la siguiente interpretación: Si, por otro lado, el presentador escoge de manera aleatoria y uniforme entre las puertas que aún no se han abierto, entonces la probabilidad que el candidato se lleve el coche (dado que él no cambia de puerta) es P[X=Y|M=cabra]=P[X=Y]/P[M=cabra]=P[X=Y]/(P[M=cabra|X=Y]P[X=Y] + P[M=cabra|X≠Y]P[X≠Y])=(1/3)/(1/3 + (1/2)*(2/3)) = 1/2. Por lo tanto, 0,5 es la probabilidad que el candidato se lleve el coche (dado que él cambia de puerta), pero esta respuesta no es aplicable a nuestro problema.